우선순위 큐(Priority Queue)란?

우선순위 큐(priority queue)

▶ 우선순위를 가진 항목들을 저장하는 큐(queue)

▶ FIFO 순서가 아니라 우선 순위가 높은 데이터가 먼저 나가게 된다.

자료구조	삭제되는 요소
스택	가장 최근에 들어온 데이터 (LIFO)
큐	가장 먼저 들어온 데이터 (FIFO)
우선순위 큐	가장 우선순위가 높은 데이터

 

환자 치료의 예시를 들어보자.

▶ 큐: 먼저 온 사람을 먼저 치료

▶ 스택: 나중에 온 사람을 먼저 치료

▶ 우선순위 큐: 위급한 사람을 먼저 치료

 

우선순위 큐(priority queue)는 가장 일반적인 큐임.

스택(stack)이나 FIFO 큐를 우선순위 큐로 구현할 수 있다.

 

우선순위

▶ 시간: 스택, 큐

▶ 스택, 큐에서는 시간에 따라 자료구조를 조직화

▶ 다른 가치: 우선순위 큐

▶ 따라서 우선순위 큐는 스택이나 큐보다 일반적인 구조

▶ 키 (= 우선순위 값) 필드가 필요

 

우선순위 큐의 추상자료형 (Abstarct Data Type)

▶ 객체: n개의 element형의 우선 순위를 가진 요소들의 모임

▶ 연산

1) create(): 우선순위 큐를 생성한다.

2) init(q): 우선순위 큐 q를 초기화한다.

3) is_empty(q): 우선순위 큐 q가 비어있는지를 검사한다.

4) is_full(q): 우선순위 큐 q가 가득 찼는가를 검사한다.

5) insert(q, x): 우선순위 큐 q에 요소 x를 추가한다.

6) delete(q): 우선순위 큐로부터 가장 우선순위가 높은 요소를 삭제하고 이 요소를 반환한다.

 

▶ 가장 중요한 연산은 insert 연산(요소 삽입), delete 연산(요소 삭제)이다.

▶ 우선순위 큐는 2가지로 구분

1) 최소 우선순위 큐

2) 최대 우선순위 큐

 

우선순위 큐 구현 방법

▶ 배열(array)을 이용한 우선순위 큐

▶ 연결리스트(linked list)를 이용한 우선순위 큐

▶ 히프(heap)를 이용한 우선순위 큐

먼저, 배열을 이용한 방법을 알아보자.

 

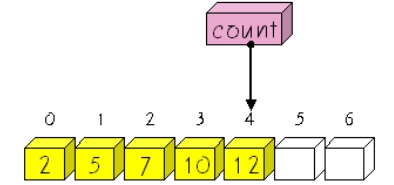
정렬된 배열(array)

▶ 우선순위를 기준으로 오름차순으로 정렬
▶ 가장 우선순위가 큰 데이터는 항상 배열의 마지막에 위치

 

삽입 함수

삽입 함수는 삽입 위치를 찾아야 함

▶ 일단 키 값을 기준으로 처음부터 삽입 위치까지 탐색. 시간 복잡도는 O(n)

▶ 해당 위치에 키 입력을 위한 데이터 이동 필요, O(n)

▶ 따라서 삽입 시, 시간 복잡도는 O(n)

 

삭제 함수

삭제 함수는 마지막 데이터를 리턴, 배열 데이터의 개수를 하나 줄임

▶ 삭제 시, 시간 복잡도는 O(1)

 

C언어로 구현해보자.

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100

typedef int element;
typedef struct {
    element data[MAX_SIZE];
    int size;
} PriorityQueue;

// 우선순위 큐 초기화
void init_queue(PriorityQueue *pq) {
    pq->size = 0;
}

// 우선순위 큐가 비었는지 확인
int is_empty(PriorityQueue *pq) {
    return pq->size == 0;
}

// 우선순위 큐가 가득 찼는지 확인
int is_full(PriorityQueue *pq) {
    return pq->size == MAX_SIZE;
}

// 우선순위 큐에 요소 삽입
void enqueue(PriorityQueue *pq, element item) {
    if (is_full(pq)) {
        fprintf(stderr, "큐가 포화상태입니다.\n");
        return;
    }
    int i = pq->size - 1;
    while (i >= 0 && pq->data[i] > item) {
        pq->data[i + 1] = pq->data[i];
        i--;
    }
    pq->data[i + 1] = item;
    pq->size++;
}

// 우선순위 큐에서 요소 삭제
element dequeue(PriorityQueue *pq) {
    if (is_empty(pq)) {
        fprintf(stderr, "큐가 공백상태입니다.\n");
        return -1; // 오류 값 반환
    }
    return pq->data[--pq->size];
}

// 우선순위 큐 출력
void print_queue(PriorityQueue *pq) {
    for (int i = 0; i < pq->size; i++) {
        printf("%d ", pq->data[i]);
    }
    printf("\n");
}

// 우선순위 큐 테스트
int main() {
    PriorityQueue pq;

    init_queue(&pq);

    enqueue(&pq, 3);
    enqueue(&pq, 1);
    enqueue(&pq, 4);
    enqueue(&pq, 1);
    enqueue(&pq, 5);
    enqueue(&pq, 9);

    printf("Priority Queue: ");
    print_queue(&pq);

    printf("Dequeue: %d\n", dequeue(&pq));
    printf("Dequeue: %d\n", dequeue(&pq));

    printf("Priority Queue after dequeue: ");
    print_queue(&pq);

    return 0;
}

 

 

정렬 안된 배열(array)

정렬되지 않은 배열은 정렬된 배열과 비교하여 삽입과 삭제 함수에서 차이를 보인다.

 

삽입 함수

삽입 함수는 새로운 데이터를 무조건 배열 끝에 붙임

▶ 삽입의 시간 복잡도는 O(1)

 

삭제 함수

삭제 함수는 삭제할 데이터를 찾아야 함

▶ 삭제 시, 가장 높은 우선 순위를 처음부터 끝까지 뒤져야 함. 시간 복잡도는 O(n)

▶ 삭제 후, 데이터 이동 필요. 시간 복잡도는 O(n)

▶ 따라서, 삭제의 시간 복잡도는 O(n)

 

C언어로 구현해보자.

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100

typedef int element;
typedef struct {
    element data[MAX_SIZE];
    int size;
} PriorityQueue;

// 우선순위 큐 초기화
void init_queue(PriorityQueue *pq) {
    pq->size = 0;
}

// 우선순위 큐가 비었는지 확인
int is_empty(PriorityQueue *pq) {
    return pq->size == 0;
}

// 우선순위 큐가 가득 찼는지 확인
int is_full(PriorityQueue *pq) {
    return pq->size == MAX_SIZE;
}

// 우선순위 큐에 요소 삽입
void enqueue(PriorityQueue *pq, element item) {
    if (is_full(pq)) {
        fprintf(stderr, "큐가 포화상태입니다.\n");
        return;
    }
    pq->data[pq->size++] = item;
}

// 우선순위 큐에서 최솟값 요소 찾기
int find_min_index(PriorityQueue *pq) {
    if (is_empty(pq)) {
        fprintf(stderr, "큐가 공백상태입니다.\n");
        return -1; // 오류 값 반환
    }
    int min_index = 0;
    for (int i = 1; i < pq->size; i++) {
        if (pq->data[i] < pq->data[min_index]) {
            min_index = i;
        }
    }
    return min_index;
}

// 우선순위 큐에서 요소 삭제
element dequeue(PriorityQueue *pq) {
    if (is_empty(pq)) {
        fprintf(stderr, "큐가 공백상태입니다.\n");
        return -1; // 오류 값 반환
    }
    int min_index = find_min_index(pq);
    element min_value = pq->data[min_index];
    // 삭제한 요소 뒤의 모든 요소를 한 칸 앞으로 이동
    for (int i = min_index; i < pq->size - 1; i++) {
        pq->data[i] = pq->data[i + 1];
    }
    pq->size--;
    return min_value;
}

// 우선순위 큐 출력
void print_queue(PriorityQueue *pq) {
    for (int i = 0; i < pq->size; i++) {
        printf("%d ", pq->data[i]);
    }
    printf("\n");
}

// 우선순위 큐 테스트
int main() {
    PriorityQueue pq;

    init_queue(&pq);

    enqueue(&pq, 3);
    enqueue(&pq, 1);
    enqueue(&pq, 4);
    enqueue(&pq, 1);
    enqueue(&pq, 5);
    enqueue(&pq, 9);

    printf("Priority Queue: ");
    print_queue(&pq);

    printf("Dequeue: %d\n", dequeue(&pq));
    printf("Dequeue: %d\n", dequeue(&pq));

    printf("Priority Queue after dequeue: ");
    print_queue(&pq);

    return 0;
}

 

 

정렬 안된 배열 VS 정렬된 배열

둘의 차이를 비교해보자.

▶ 정렬된 배열과 정렬 안된 배열을 사용할 때의 삽입, 삭제 효율이 서로 뒤바뀐 모습

▶ 삭제가 빨라야 한다면 정렬된 배열을 사용

▶ 삽입이 빨라야 한다면 정렬 안된 배열을 사용

▶ 삽입 삭제 전체를 감안하면 두 방법 모두 O(n)의 시간 복잡도이다.

그 다음, 연결 리스트를 이용한 우선순위 큐 구현 방법을 알아보자.

 

정렬된 연결 리스트(linked list)에 의한 구현

▶ 우선순위를 기준으로 내림차순으로 정렬

▶ 우선순위가 가장 높은 데이터를 헤드 포인터가 직접 가리킴

▶ 삭제의 시간 복잡도는 O(1)

▶ 삽입 함수는 키 값을 기준으로 삽입 위치를 찾아야 함.

▶ 삽입 위치가 마지막일 경우가 최악의 경우임. 시간 복잡도는 O(n)

▶ 배열처럼 이동은 불필요. 포인터만 변경하면 됨

▶ 삭제와 삽입 모두를 감안한 시간 복잡도는 O(1) + O(n) = O(n)이다.

 

C언어로 구현해보자.

#include <stdio.h>
#include <stdlib.h>

typedef int element;
typedef struct Node {
    element data;
    struct Node* next;
} Node;

typedef struct {
    Node* head;
} PriorityQueue;

// 우선순위 큐 초기화
void init_queue(PriorityQueue* pq) {
    pq->head = NULL;
}

// 우선순위 큐가 비었는지 확인
int is_empty(PriorityQueue* pq) {
    return pq->head == NULL;
}

// 우선순위 큐에 요소 삽입
void enqueue(PriorityQueue* pq, element item) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    new_node->data = item;
    new_node->next = NULL;

    // 정렬된 위치에 삽입
    if (is_empty(pq) || pq->head->data > item) {
        new_node->next = pq->head;
        pq->head = new_node;
    } else {
        Node* current = pq->head;
        while (current->next != NULL && current->next->data <= item) {
            current = current->next;
        }
        new_node->next = current->next;
        current->next = new_node;
    }
}

// 우선순위 큐에서 요소 삭제
element dequeue(PriorityQueue* pq) {
    if (is_empty(pq)) {
        fprintf(stderr, "큐가 공백상태입니다.\n");
        return -1; // 오류 값 반환
    }
    Node* temp = pq->head;
    element min_value = temp->data;
    pq->head = pq->head->next;
    free(temp);
    return min_value;
}

// 우선순위 큐 출력
void print_queue(PriorityQueue* pq) {
    Node* current = pq->head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

// 우선순위 큐 테스트
int main() {
    PriorityQueue pq;
    init_queue(&pq);

    enqueue(&pq, 3);
    enqueue(&pq, 1);
    enqueue(&pq, 4);
    enqueue(&pq, 1);
    enqueue(&pq, 5);
    enqueue(&pq, 9);

    printf("Priority Queue: ");
    print_queue(&pq);

    printf("Dequeue: %d\n", dequeue(&pq));
    printf("Dequeue: %d\n", dequeue(&pq));

    printf("Priority Queue after dequeue: ");
    print_queue(&pq);

    return 0;
}

 

 

정렬 안된 연결 리스트(linked list)에 의한 구현

▶ 삽입될 데이터를 가장 첫 노드에 삽입. 시간 복잡도는 O(1)
▶ 배열처럼 이동은 불필요. 포인터만 변경하면 됨.

▶ 삭제를 위해 가장 큰 데이터를 처음부터 마지막까지 탐색해야 함. 탐색의 시간 복잡도는 O(n)

▶ 삭제와 삽입 모두를 감안한 시간 복잡도는 O(n) + O(1) = O(n)

 

C언어로 구현해보자.

#include <stdio.h>
#include <stdlib.h>

typedef int element;
typedef struct Node {
    element data;
    struct Node* next;
} Node;

typedef struct {
    Node* head;
} PriorityQueue;

// 우선순위 큐 초기화
void init_queue(PriorityQueue* pq) {
    pq->head = NULL;
}

// 우선순위 큐가 비었는지 확인
int is_empty(PriorityQueue* pq) {
    return pq->head == NULL;
}

// 우선순위 큐에 요소 삽입
void enqueue(PriorityQueue* pq, element item) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    new_node->data = item;
    new_node->next = pq->head;
    pq->head = new_node;
}

// 우선순위 큐에서 최솟값 요소 찾기
Node* find_min_node(PriorityQueue* pq) {
    if (is_empty(pq)) {
        return NULL;
    }

    Node* min_node = pq->head;
    Node* current = pq->head;
    while (current != NULL) {
        if (current->data < min_node->data) {
            min_node = current;
        }
        current = current->next;
    }
    return min_node;
}

// 우선순위 큐에서 요소 삭제
element dequeue(PriorityQueue* pq) {
    if (is_empty(pq)) {
        fprintf(stderr, "큐가 공백상태입니다.\n");
        return -1; // 오류 값 반환
    }

    Node* min_node = find_min_node(pq);
    element min_value = min_node->data;

    // 최솟값 노드를 삭제
    if (min_node == pq->head) {
        pq->head = pq->head->next;
    } else {
        Node* current = pq->head;
        while (current->next != min_node) {
            current = current->next;
        }
        current->next = min_node->next;
    }
    free(min_node);
    return min_value;
}

// 우선순위 큐 출력
void print_queue(PriorityQueue* pq) {
    Node* current = pq->head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

// 우선순위 큐 테스트
int main() {
    PriorityQueue pq;
    init_queue(&pq);

    enqueue(&pq, 3);
    enqueue(&pq, 1);
    enqueue(&pq, 4);
    enqueue(&pq, 1);
    enqueue(&pq, 5);
    enqueue(&pq, 9);

    printf("Priority Queue: ");
    print_queue(&pq);

    printf("Dequeue: %d\n", dequeue(&pq));
    printf("Dequeue: %d\n", dequeue(&pq));

    printf("Priority Queue after dequeue: ");
    print_queue(&pq);

    return 0;
}

 

각 구현 방법에 따른 성능을 비교해보자. (시간 복잡도)

표현 방법	삽입	삭제
정렬 안된 배열	O(1)	O(n)
정렬 안된 연결 리스트	O(1)	O(n)
정렬된 배열	O(n)	O(1)
정렬된 연결 리스트	O(n)	O(1)
히프 (heap)	O(logn)	O(logn)

 

▶ n이 1000일 경우, O(n) 알고리즘은 1000초, O(logn) 알고리즘은 10초가 소요된다.

 

히프(heap)에 대해서는 다음 게시글에서 다뤄보도록 하겠다.

 

 

다음에 계속...